Maxwell’s Equations

In vacuum:

In a medium:

Classical Treatment of Magnetic Materials

Time-Varying E Field

The electric field

The polarization drift

Time Varying B Field

The magnetic field

The magnetic moment is invariant in slowly varying magnetic fields

The magnetic flux through a Larmor orbit is constant

• $\Phi$ is constant if $\mu$ is constant.

The First Adiabatic Invariant, $\mu$

The Second Adiabatic Invariant, J

The Third Adiabatic Invariant, $\Phi$

Interplay between ML and Physics

Governing equantion
Conservation law
Symmetry

Importance of Conservation and symmetry

Overview

AI Poincare

1D Harmonic Oscillator

2D Kepler Problem

Conservation Law & Manifold

Coordinatizations of spacetime

Intuitively, an “event” is “something which happens at a definite place at a definite time”.

The set $\mathbf E$ of all events is called spacetime.

coordinatization of $\mathbf E$

E onto the four-dimensional real vector space $R^4$

Lorentz coordinatizations

Properties

(1)For any stationary standard clock with coordinates $(t(\tau),x_0,y_0,z_0),t(\tau)=\tau$ for all $\tau$.

(2)Light always moves in straight lines with unit velocity.The function $t\longmapsto\overrightarrow{r}(t)$ is of the form $\overrightarrow{r}(t)=\overrightarrow{v}t+\overrightarrow{r_0}$, where $\overrightarrow{v},\overrightarrow{r_0}\in R^3$ are constant vectors, and $\overrightarrow{v}$ is a unit vector.

Minkowski space

Minkowski metric

$$<u,v>:=u^0v^0-u^1v^1-u^2v^2-u^3v^3$$

Lorentz transformations

Preprocessing data using different techniques

Getting ready

1
2
3
4

import numpy as np
from sklearn import preprocessing 

data = np.array([[3, -1.5, 2, -5.4], [0, 4, -0.3, 2.1], [1, 3.3, -1.9, -4.3]]) ~~~~

How to do it…

1
2
3
4

# Mean removal
data_standardized = preprocessing.scale(data)
print "\nMean =", data_standardized.mean(axis=0)
print "Std deviation =", data_standardized.std(axis=0)

• python preprocessor.py

Mean = [ 5.55111512e-17 -1.11022302e-16 -7.40148683e-17 -7.40148683e-17]

Std deviation = [ 1. 1. 1. 1.]

1
2
3
4

# Scaling 
data_scaler = preprocessing.MinMaxScaler(feature_range=(0.1))
data_scaled = data_scaler.fit_transform(data)
print "\nMin max scaled data =", data_scaled 

1
2
3

# Normalization
data_normalized = preprocessing.normalize(data, norm='l1')
print "\nL1 normalized data =", data_normalized

1
2
3

# Binarization
data_binarized = preprocessing.Binarizer(threshold=1.4).transform(data)
print "\nBinarized data =", data_binarized

>

1
2
3
4
5

# One Hot Encoding
encoder = preprocessing.OneHotEncoder()
encoder.fit([[0, 2, 1, 12], [1, 3, 5, 3], [2, 3, 2, 12],[1, 2, 4, 3]])
encoded_vector = encoder.transform([[2, 3, 5, 3]]).toarray()
print "\nEncoded vector =", encoded_vector

Label encoding

How to do it…

1
2
3
4
5
6

from sklearn import preprocessing
label_encoder = preprocessing.LabelEncoder()
input_classes = ['audi', 'ford', 'audi', 'toyota', 'ford', 'bmw']
label_encoder.fit(input_classes)
print "\nClass mapping:"
for i, item in enumerate(label_encoder.classes_): print item, '-->', i

>

1

labels =

Nonuniform B Field

$\nabla B\perp B:\ Grad-B\ Drift$

The guiding center drift velocity

$The\ grad-\mathbf B\ drift$

Curved B: Curvature Drift

The centrifugal force

The curvature drift velocity

The total drift

$\nabla B||B$: Magnetic Mirrors

The magnetic moment of the gyrating particle

The average force

A plasma trapped between magnetic mirrors

Nonuniform E Field

The electric field

The equation of motion

The finite-Larmor-radius effect

holomorphicity

A function $f:\mathbb C\rightarrow\mathbb C$ is holomorphic at the point $z\in\mathbb C$ if the limit

exists.

characteristic properties of holomorphic functions

• Contour integration: If f is holomorphic in $\Omega$,then for appropriate closed paths in $\Omega$

  $$\int_\gamma f(z)dz=0$$

• Regularity: If f is holomorphic, then f is indefinitely differentiable.

• Analytic continuation: If f and g are holomorphic functions in $\Omega$ which are equal in an arbitrarily small disc in $\Omega$,then f=g everywhere in $\Omega$.

• The zeta function

  $$\zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s}$$

• The theta function

  $$\Theta(z|\tau)=\sum_{n=-\infty}^{\infty}e^{\pi in^2}e^{2\pi inz}$$

• Basic properties

The complex plane

Commutativity

Associativity

Distributivity

The absolute value

The triangle inequality

The complex conjugate

In polar form

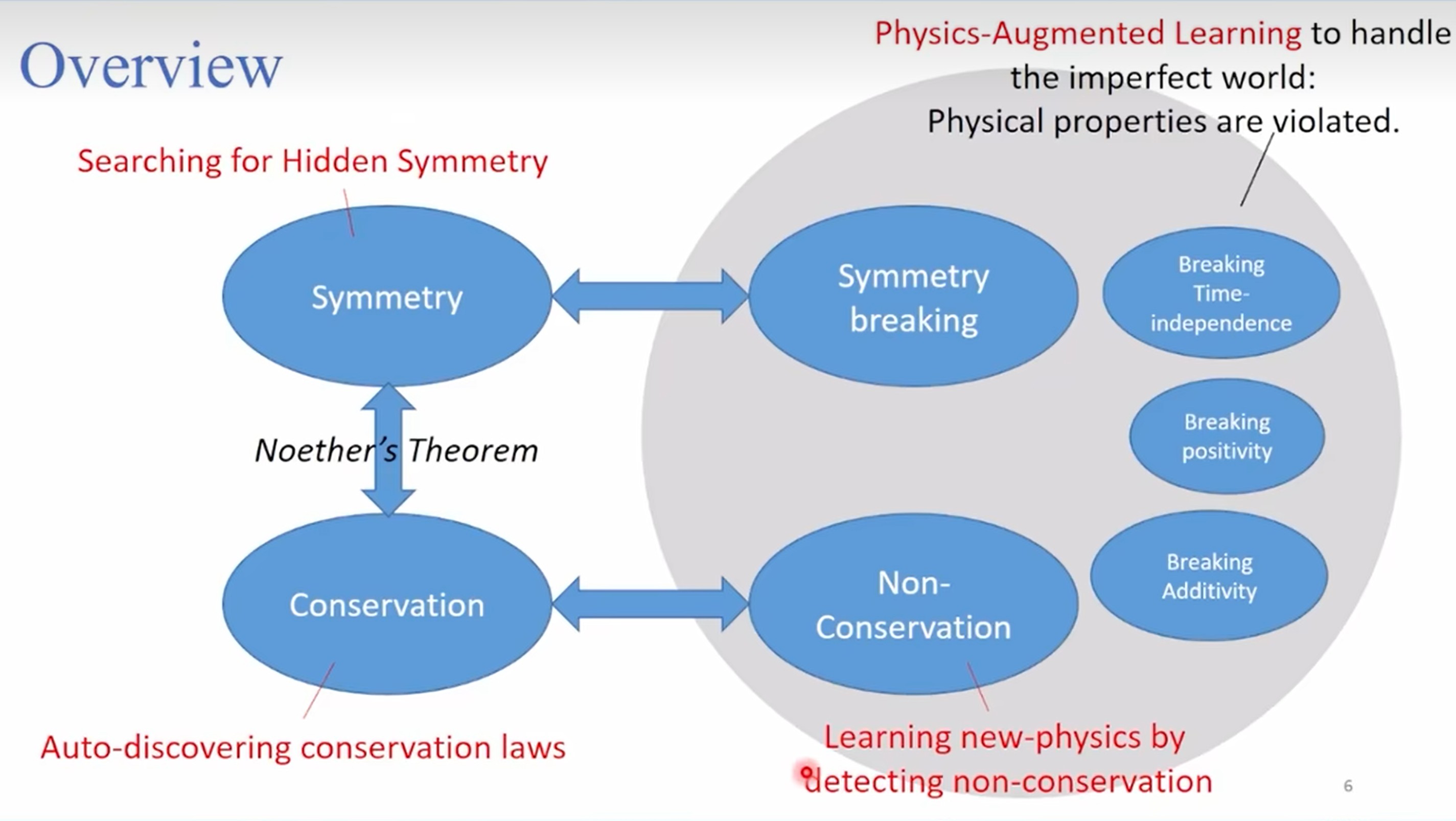
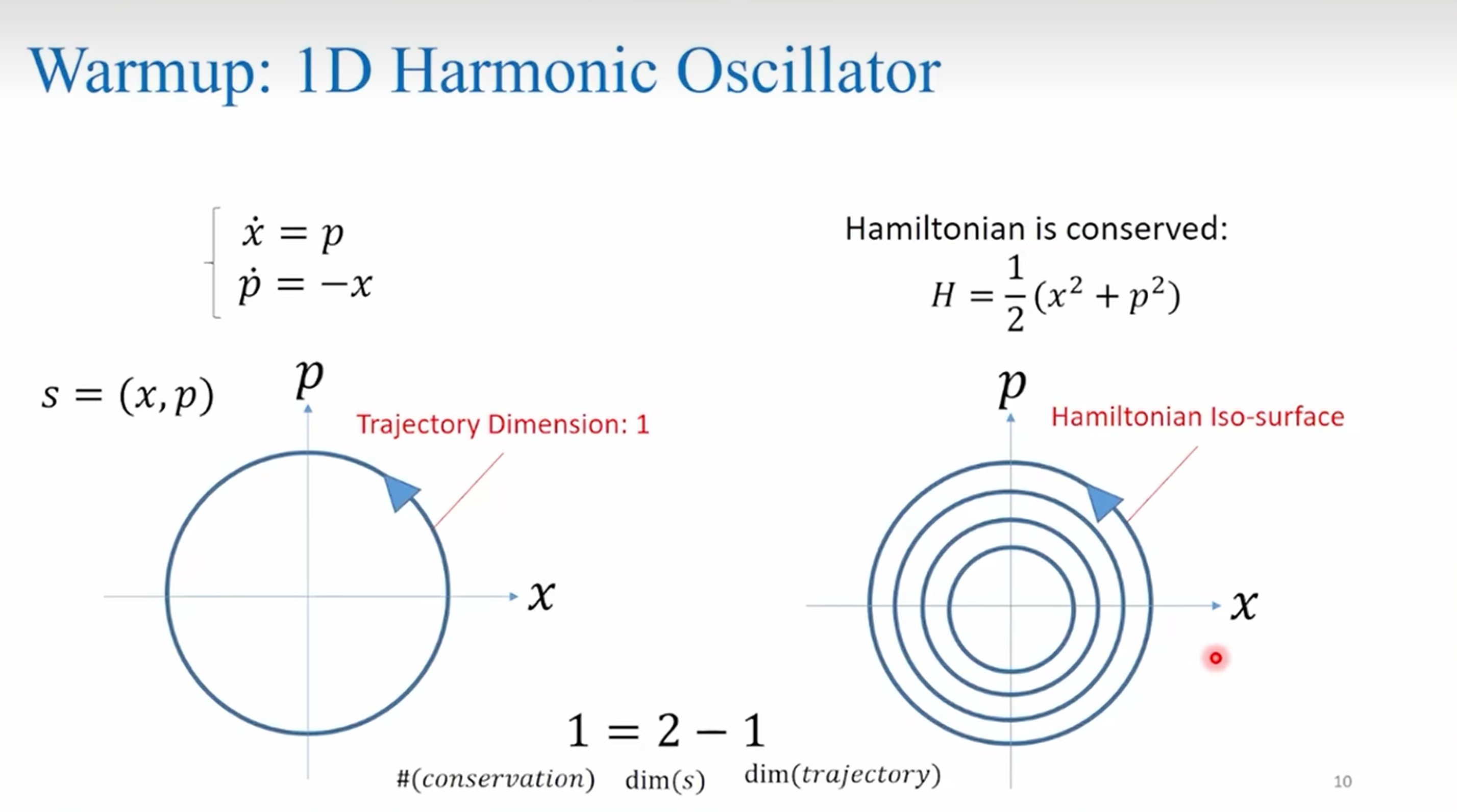
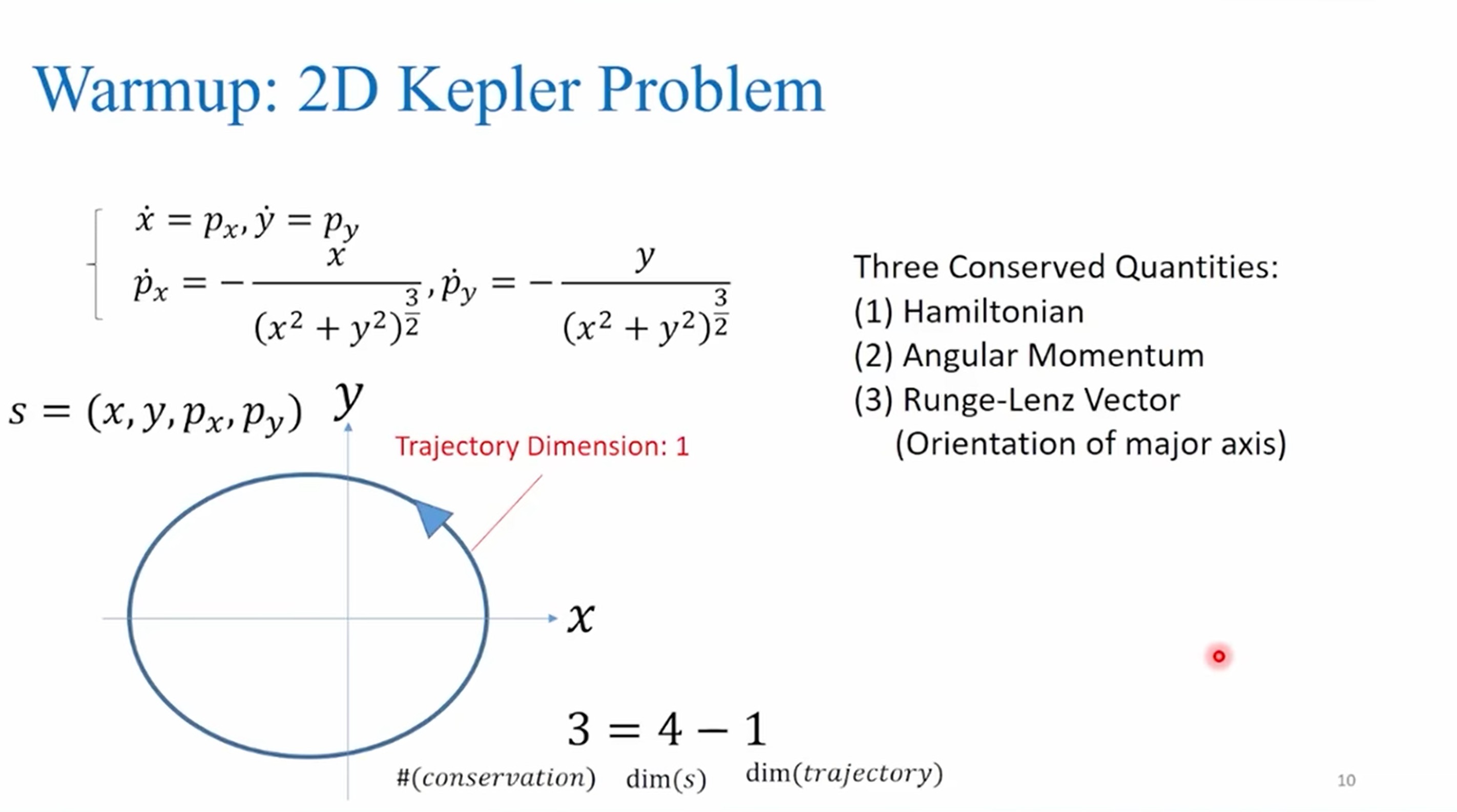
The prime number theory

Lemma 1

Every nonzero integer can be written as a product of primes.

Theorem 1

For every nonzero integer n there is a prime factorization

with the exponents uniquely determined by n.

Lemma 2

If$a,b\in \mathbb{Z}$ and b>0, there exist q,r\in\mathbb{Z}such that a=qb+r with $0\leq r<b$

Definition

If $a_1, a_2,...,a_n\in\mathbb{Z}$, we define $(a_1, a_2,..., a_n)$ to be the set of all integers of the form $a_1x_1+a_2x_2++a_nx_n$ with $x_1, x_2, \cdots, x_n\in \mathbb Z$.

Lemma 3

If $a,b\in\mathbb Z$, then there is a $d\in\mathbb Z$ such that (a,b)=(d).

Definition

Let $a,b\in\mathbb Z$. An integer d is called a greatest common divisor of a and b if d is a divisor of both a and b and if every other common divisor of a and b divides d.

Lemma 4

Let $a,b\in\mathbb Z$.If (a,b)=(d) then d is a greatest common divisor of a and b.

Definition

We say that two integers a and b are relatively prime if the only common divisors are $\pm 1$, the units.

Proposition 1.1.1

Suppose that a|bc and that (a,b)=1.Then a|c.

Corollary 1

If p is a prime and p|bc, then either p|b or p|c.

Corollary 2

Suppose that p is a prime and that $a,b\in\mathbb Z$. Then $ord_pab=ord_pa+ord_pb$.

Unique Factorization in k[x]

Reference book
A Classical Introduction to Modern Number Theory by Kenneth Ireland and Michael Rosen

Linear Algebra

• Scalar

• Vector

  $$\mathbf x=\begin{bmatrix} x_1\\x_2\\ \vdots\\x_n \end{bmatrix}$$

• The $L_p$ norm of a vector

• The $L_1$ norm of a vector

• The $L_2$ norm of a vector

• The $L_\infty$ norm of a vector

• The distance of two vectors $\mathbf x_1,\mathbf x_2$

• A set of vectors $\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_m$ are linearly independent

not exist a set of scalars $\lambda_1,\lambda_2,\cdots,\lambda_m,$ which are not all 0

• Matrix

  $$\mathbf A=\begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m1}&a_{m2}&\cdots&a_{mn} \end{bmatrix}$$

• Matrix product

  $$\mathbf A\in\mathbb R^{m\times n}$$ $$\mathbf B\in\mathbb R^{n\times p}$$ $$\mathbf C_{ij}=\sum_{k=1}^{n}\mathbf A_{ik}\mathbf B_{kj}$$ $$\mathbf C\in\mathbb R^{m\times p}$$

• determinant

  $$det(\mathbf A)=\sum_{k_1k_2\cdots k_n}(-1)^{\tau(k_1k_2\cdots k_n)} a_{1k_1}a_{2k_2}\cdots a_{nk_n}$$ $$k_1k_2\cdots k_n\ is\ a\ permutation\ of\ 1,2,\cdots,n$$ $$\tau(k_1k_2\cdots k_n)\ is\ the\ inversion\ number\ of\ the\ permutationk_1k_2\cdots k_n$$

• The inverse matrix

  $$\mathbf A^{-1}\mathbf A=\mathbf I$$

• The transpose of matrix

  $$\mathbf A_{ij}^{T}=\mathbf A_{ji}$$

• The Hadamard product

  $$\mathbf A\in\mathbb R^{m\times n}$$ $$\mathbf B\in\mathbb R^{m\times n}$$ $$\mathbf C_{ij}=\mathbf A_{ij}\mathbf B_{ij}$$ $$\mathbf C\in\mathbb R^{m\times n}$$

• Tensor: An array with arbitrary dimension

Probability theory

• joint probability

  $$P(X=x_1,Y=y_1)$$

• conditional probability

  $$P(X=x_1|Y=y_1)$$

• The sum rule

  $$P(X=x)=\sum_yP(X=x,Y=y)$$

• The product rule

  $$P(X=x,Y=y)=P(Y=y|X=x)P(X=x)$$

• Bayes formula

  $$P(Y=y|X=x)=\frac{P(X=x,Y=y)}{P(X=x)}=\frac{P(X=x|Y=y)P(Y=y)}{P(X=x)}$$ $$P(X_i=x_i|Y=y)=\frac{P(Y=y|X_i=x_i)P(X_i=x_i)}{\sum_{j=1}^nP(Y=y|X_j=x_j)}$$

• The chain rule

  $$P(X_1=x_1,\cdots,X_n=x_n)\\ =P(X_1=x_1)\prod_{i=2}^{n}P(X_i=x_i|X_1=x_1,\cdots,X_{i-1}=x_{i-1})$$

• The expectation of f(x)

  $$\mathbb E[f(x)]=\sum_xP(x)f(x)$$

• The variance of f(x)

  $$\begin{aligned} Var(f(x)&=\mathbb E[(f(x)-\mathbb E[f(x)])^2]\\ &=\mathbb E[f(x)^2]-\mathbb E[f(x)]^2 \end{aligned}$$

• The standard deviation

  $$\sqrt{Var(f(x)}$$

• Covariance

  $$Cov(f(x),g(y))=\mathbb E[(f(x)-\mathbb E[f(x)])(g(y)-\mathbb E[g(y)])]$$

• Gaussian distribution

  $$N(x|\mu,\sigma^2)=\sqrt{\frac{1}{2\pi\sigma^2}}exp(-\frac{1}{2\sigma^2}(x-\mu)^2)$$ $$\mu\ is\ the\ mean\ of\ variable\ x$$ $$\sigma^2\ is\ the\ variance$$

• Bernoulli distribution

  $$P(X=x)=p^x(1-p)^{(1-x)},x \in \left\{0,1\right\}$$

• Binomial distribution

  $$P(Y=k)=\begin{pmatrix}N\\k\end{pmatrix}p^k(1-p)^{(N-k)}$$

• Laplace distribution

  $$P(x|\mu,b)=\frac{1}{2b}exp(-\frac{\lvert x -\mu\rvert}{b})$$

Graph theory

• Adjacency matrix

  $$A_{ij}=\left\{ \begin{aligned} &1\ if\left\{v_i,\ v_j\right\}\in E\ and\ i\ \neq\ j,\\ &0\ otherwise. \end{aligned} \right.$$

• Degree matrix

  $$D_{ii}=d(v_i)$$

• Laplacian matrix

  $$L=D-A$$ $$L_{ij}=\left\{ \begin{aligned} &d(v_i)\ if\ i=j,\\ &-1\ if\left\{v_i,v_j\right\}\in E\ and\ i\ \neq\ j,\\ &0\ otherwise. \end{aligned} \right.$$

• Symmetric normalized Laplacian

  $$\begin{aligned} L^{sym}&=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}\\ &=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \end{aligned}$$

• Random walk normalized Laplacian $$L^{rw}=D^{-1}L=I-D^{-1}A$$ $$L_{ij}^{rw}= \left\{ \begin{aligned} &1\ if\ i=j\ and\ d(v_i)\ \neq\ 0,\\ &-\frac{1}{d(v_i)}\ if\left\{v_i,v_j\right\}\in E\ and\ i\ \neq\ j,\\ &0\ otherwise. \end{aligned} \right.$$
• Incidence matrix

For a directed graph

For a undirected graph

General formalism

The state space of a system of N distinguishable particles

• The space of the completely symmetric states for bosons $\varepsilon_S(N)$

The projectors

$$S_N=\frac{1}{N!}\sum_\alpha P_\alpha$$

• The space of the completely antisymmetric states for fermions $\varepsilon_A(N)$

The projectors

$$A_N=\frac{1}{N!}\sum_\alpha\varepsilon_\alpha P_\alpha$$

• The $P_\alpha$ is the N! permutation operators for the N particles

• The $\varepsilon_\alpha$ is the parity of $P_\alpha$

• The subscript $\alpha$ distinguishes the different permutations of the N particles, and therefore take N! different values

Fock states for identical bosons

• The subscripts i, j, k, l, ..denote different basis vectors {$|u_i\rangle$} of the state space $\varepsilon_1$ of a single particle